风格迁移-生成图片
画由心生,境为意造 —— 白居易
去年《你的名字》火了之后，某 APP 发布了一个风格迁移的滤镜，随后朋友圈火了一把动画风的图片秀。当时就像玩玩风格迁移，然后这个拖延症一直至今，前几天看吴恩达的深度学习课程，突然想起这个坑。我也不知道在忙到爆炸的毕设中期前哪来的勇气这么浪去玩其他(￣.￣)
# 风格迁移简介
风格迁移（Style Transfer）是深度学习非常好玩的一个应用，它可以从一张图片获得风格，另一张图片或得内容，再合成为一张新的图片，比如：
左上角是需要的内容图片，右上角是想要学习的风格图片，想要学习、生成下面的新图片。
卷积神经网络中学习到了什么
对于图片分类，我们一般使用卷积神经网络获取图片信息，最终输出类别，比如下图中的网络，其实就是一层层的堆积卷积层和池化层，最后加几个全连接层：
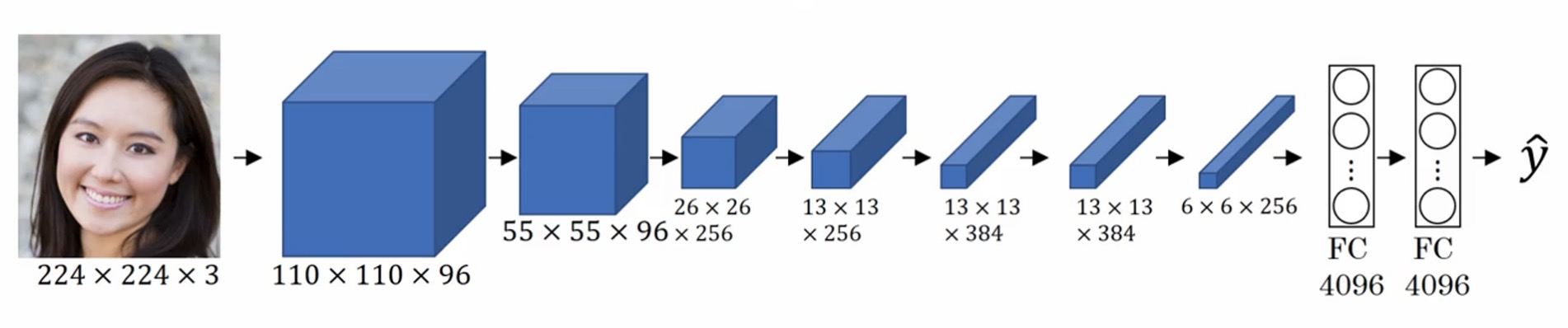我们常说，在深度神经网络中，浅层的神经元拟合简单的信息，深层的拟合更复杂的信息。那么在 CNN 中，每层卷积核分别在什么情况下激活呢？下图是上面的网络，每层卷积核激活时候的输入输入：
可以看出，浅层的核只是拟合简单的线条，越是深层拟合的东西越复杂（可以想象卷积核移动的时候，浅层往往只关注局部的信息，而越是深层，对于输入图像关注的范围越大）。
在我们的生成迁移模型中，将会使用预训练好的 CNN 网络模型，来提取图形特征与内容，使用越深的网络获取到的特征越高层，因此选用较浅的层将会更加像素级的趋近输入图片，越深则越在内容上趋近。
风格迁移模型
最早期的风格迁移模型非常缓慢，因为它把图片的生成过程当做一个“训练”过程，将风格图片和内容图片作为输入，生成最后的新图片，每生成一张图片都相当于训练一个模型。模型图如下：
因此我们需要加快风格迁移的速度，需要把其当做一个“生成”或者“执行”的过程，即快速风格迁移，该模型图如下：
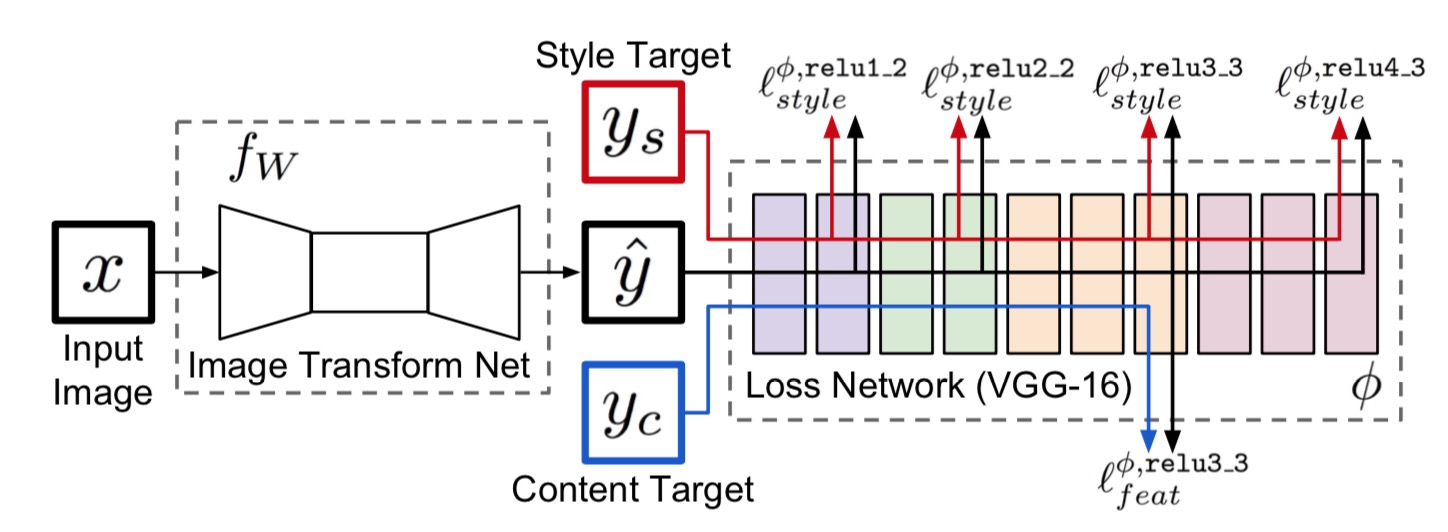首先随机生成一张图片 G，然后通过前面提到的网络选择出某特征层l，将内容图片和风格图片通过同样的方式得到某个特征层，再按照下面的方法得到损失函数进而通过反向传播修改 G。可以简化为如图所示：
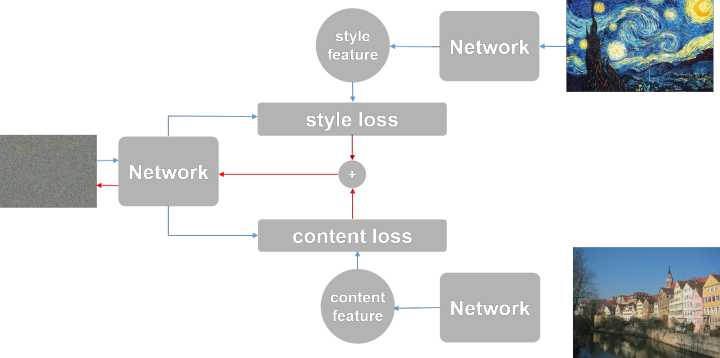蓝色箭头为前向运算，红色箭头为反向运算，三个 Network 其实是同一个。
损失函数
训练机器学习模型，需要定义损失函数。从上面对风格迁移模型的描述可以看出，模型的损失由两部分来定义：内容损失与风格损失，即：
$$J(G) = \alpha J_{Content}(C,G) + \beta J_{Style}(S,G)$$
其中，C(Content)表示内容图片，S(Style)表示风格图片，G(Generate)即第一项表示内容的损失，第二项表示风格的损失。
内容损失函数
那么如何来计算内容损失函数$\alpha J_{Content}(C,G)$呢？
首先应该使用一个预训练好的卷积神经网络模型，比如 VGG19，然后选择 l 层的激活来计算生成图片 G 和内容图片 C 的相似性，即计算 $a^{[l](C)}$ 和 $a^{[l](G)}$之间的相似度。这两个值越相似，那么 G 和 C 的内容就越相似。
$$J_{Content}(C,G) = \frac{1}{2} \lVert a^{[l](C)} - a^{[l](G)} \rVert^2$$
风格损失函数
首先我们需要定义什么是风格。风格就是 l 层中不同通道的激活值的相关性。因为不同通道的卷积核，对不同的特征敏感，那么如果多个通道同时激活，说明图中出现了某些关联的特征，即风格。例如对于某层（l层）激活值的维度为：$n_H, n_W, n_C$，$a^{[l]}_{i,j,k}$表示$(i,j,k)$上的激活值，$G^{[l](S)}$表示风格矩阵，它是一个$n^{[l]}_C \times n^{[l]}C$维度的矩阵。$G^{[l](S)}{kk’}$表示在 k 通道和 k’ 通道的关联性：
$$G^{[l](S)}{kk’} = \sum{i=1}^{n_H^{[l]}} \sum_{j=1}^{n_w^{[l]}} a^{[l]}{i,j,k} a^{[l]}{i,j,k’}$$
进而，风格损失函数可以定义为：
$$J_{Stype}^{[l]}(S,G) = \frac{1}{2n_H^{[l]}n_W^{[l]}n_C^{[l]}} \sum_k \sum_{k’}\lVert G^{[l](S)}{kk’} - G^{[l](G)}{kk’} \rVert$$
对多个层求风格损失并且累加，可以同时得到多层的风格相似性，往往效果更好：
$$J_{Style}(S,G) = \sum_l \lambda^{[l]}J_{Stype}^{[l]}(S,G)$$
模型示例
模型的代码具体见：Keras 官方 examples
这里给出几个运行的例子（从左到右依次是 风格图、内容图、生成图）：
