调参工程学 - 梯度下降优化方法
梯度下降是一个最优化算法。在深度学习中，通过梯度下降来找到损失函数的（局部）最小值，进而获得各个参数的值。
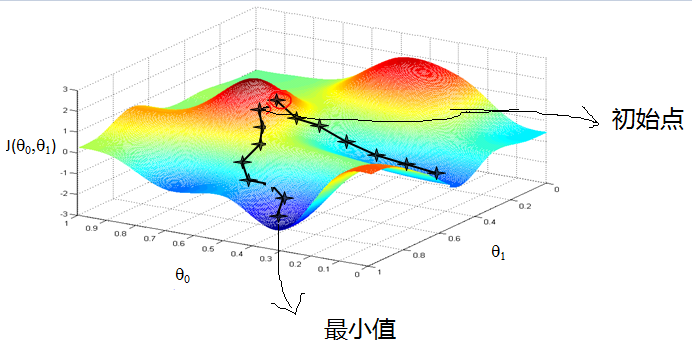
梯度下降最直观的解释如图所示，在山上某处，沿着最陡的方向向下，直到能到达的最低点。
虽然各个深度学习框架封装了若干常用的梯度下降算法，可以当做黑盒来使用，但是作为调参工程师，这些东西原理都不懂还怎么愉快的调参。
对于一般线性回归函数，其假设为：
$$h_{\theta}=\sum_{j=0}^{n}\theta_{j}x_{j}$$
对应的损失函数为：
$$J_{train}(\theta)=\frac{1}{2m}\sum_{i=1}^{m}(h_{\theta}(x^{(i)})-y^{(i)})^{2}$$
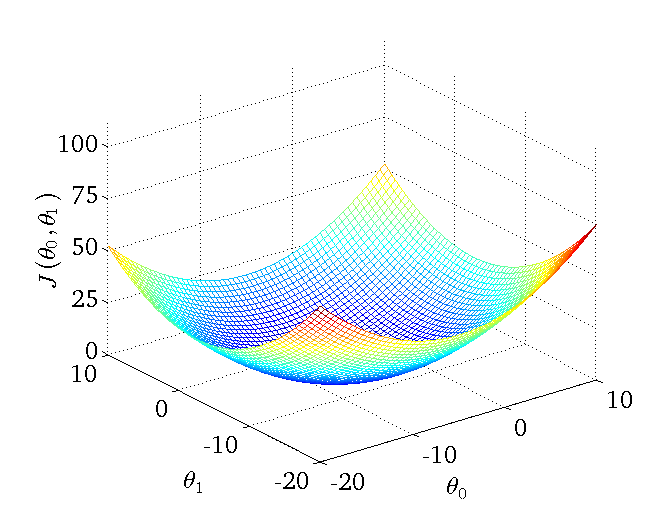
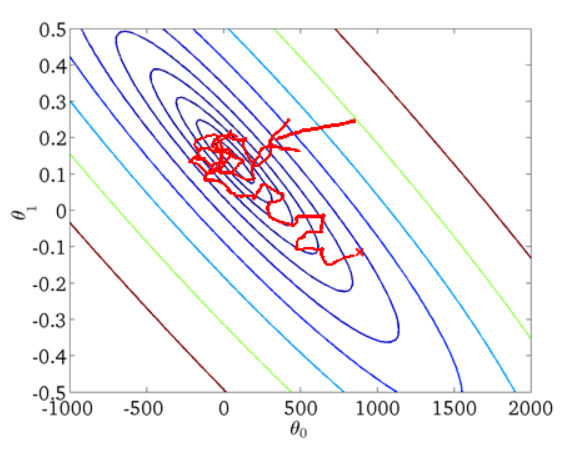
我们假设参数$\theta$是二维的，下图为一个二维参数（$\theta_{0}$和$\theta_{1}$）组对应能量函数的可视化图：
本文大概分为：基本的梯度下降算法和梯度下降优化算法。
基本的梯度下降算法
批量梯度下降（Batch Graduebt Descent, BGD）
批量梯度下降算法使用整个数据集，算得整个数据集的损失，对目标参数$\theta$求导，用来更新$\theta$：
$$\theta = \theta - \alpha\nabla_{\theta}{J(\theta)}$$
其具体的过称为：
对上面的损失函数求偏导：
$$\frac{\partial{J(\theta)}}{\partial{\theta_j}} = - \frac{1}{m}\sum_{i=1}^{m}(y^i - h_{\theta}(x^i))x_{j}^{i}$$
最小化损失函数，按照每个参数$\theta$的梯度负方向来更新每个$\theta$：
$$\theta_{j} = \theta_{j} + \alpha\frac{1}{m}\sum_{i=1}^{m}(y^i - h_{\theta}(x^i))x_{j}^{i}$$
这种方法，每更新一次参数，需要对整个数据集进行运算，十分缓慢并且非常占内存，而且不能实时在线更新参数。这是最原始的梯度下降方法。从迭代的次数上来看，BGD迭代的次数相对较少。其迭代的收敛曲线示意图可以表示如下：
随机梯度下降（Stochatic Gradient Decent, SGD）
随机梯度下降一次只使用一个样本进行目标函数梯度计算，其公式为：
$$\theta = \theta - \alpha\nabla_{\theta}{J(\theta;x^i,j^i)}$$
即将上面的损失函数改写为：
$$J_{train}(\theta)=\frac{1}{m}\sum_{i=1}^{m}\frac{1}{2}(h_{\theta}(x^{(i)})-y^{(i)})^{2} = \frac{1}{m}\sum_{i=1}^{m}cost(\theta;x^i,j^i)$$
$$cost(\theta;x^i,j^i) = \frac{1}{2}(h_{\theta}(x^{(i)})-y^{(i)})^{2}$$
利用每个样本的损失函数对$\theta$求偏导得到对应的梯度，来更新$\theta$：
$$\theta_{j} = \theta_{j} + \alpha(y^i - h_{\theta}(x^i))x_{j}^{i}$$
随机梯度下降是通过每个样本来迭代更新一次，计算非常快并且适合线上更新模型。但是，SGD伴随的一个问题是噪音较BGD要多，使得SGD并不是每次迭代都向着整体最优化方向，在解空间的搜索过程看起来很盲目。其迭代的收敛曲线示意图可以表示如下：
## 小批量梯度下降（Mini-Batch Gradient Descent, MBGD）
上述两种方法，BGD 样本多时，训练慢，占内存；SGD 找到的解却不如 BGD，并且干扰较大，不易于并行实现。而 MBGD 则是在二者之间找到一个平衡。它一次以小批量的训练数据计算目标函数的权重并更新参数。公式如下：
$$\theta = \theta - \alpha\nabla_{\theta}{J(\theta;x^{(i:i+n)},j^{(i:i+n)})}$$
其中，n为每批训练集的数量，一般设为50到256。
虽然 MBGD 相对 BGD 和 SGD 更加优秀，但是仍然存在许多问题，比如：
- 难以选择合适的学习速率：学习速率过小会造成网络收敛太慢，但是太大使得损失函数可能在最小点周围不断摇摆而永远达不到最小点；
- 可以随着训练降低学习率，虽然这个方法有一些作用，但是由于降低学习率的周期是人为事先设定的，所以它不能很好地适应数据内在的规律；
- 对特征向量中的所有的特征都采用了相同的学习率，如果训练数据十分稀疏并且不同特征的变化频率差别很大，这时候对变化频率慢得特征采用大的学习率而对变化频率快的特征采用小的学习率是更好的选择；
- 可能出现在垂直于优化方向上的摆动。
因此我们需要更好的方法来进行梯度下降的求解。
梯度下降优化算法
Momentum
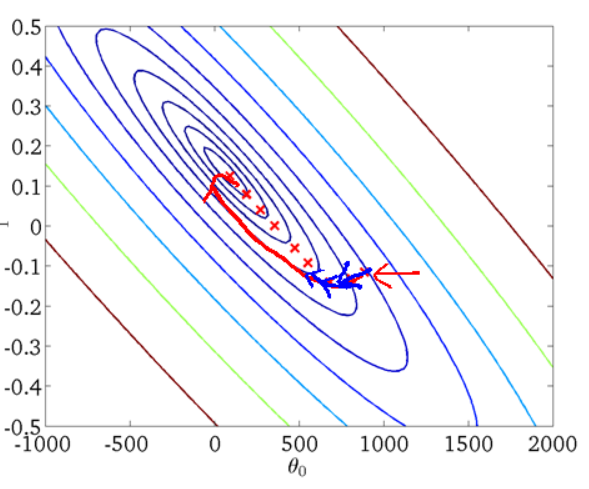
对于如图所示的损失函数等高线图：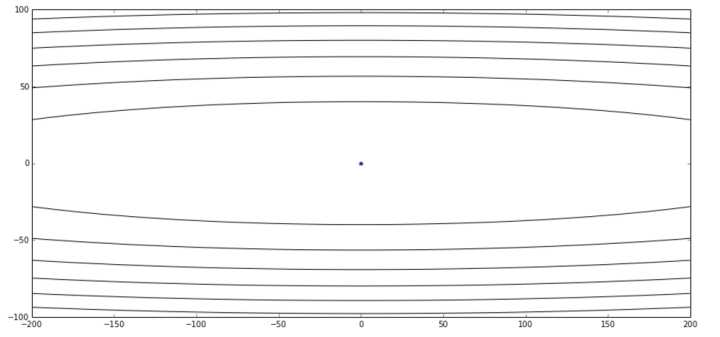
其中中心的蓝色点表示了最优值。如图我们可以知道，其在 Y 轴比较陡峭，在 X 轴比较平缓。如果我们使用普通的梯度下降方法，如果选取较小的学习效率，则其收敛的图像如下面的第一张图。可以看出我们从某个点出发，整体趋势向着最优点前进，但是其在 Y 轴变化比较快，但是在 X 轴的前进非常缓慢。如果我们增大学习效率，则如第二张图，在 Y 轴抖动非常明显：
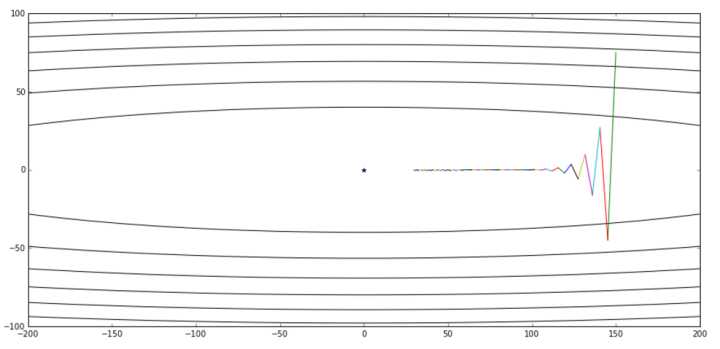
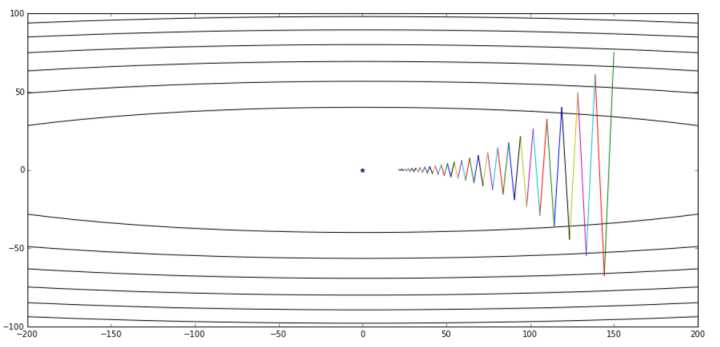在梯度下降算法中，如果学习速率选择较大，对于陡峭方向（维度）的优化，会来回的抖动，但是如果学习速率选择较小，那么对于平缓方向（维度），会异常缓慢，非常像下图：
即上面所说的第三条，如果不同维度选择的学习速率一样，可能导致陡峭维度的收敛图像来回摆动。因此很显然，我们应该尽可能的约束掉这样的维度的学习，而尽可能的往我们的目标方向前进。
指数加权平均
对于一组连续的数值，比如温度，可能变化（波动）较大，如下图的蓝色点。如果我们想要拟合温度，我们需要一个较为平缓的曲线（红色）。
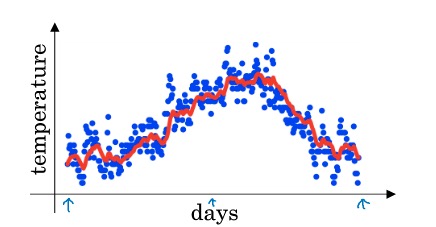如何求得这个平缓的曲线呢？我们应该想到，尽可能的平均一下前后的温度。指数平均加权是这样的思路，一个时刻的值，与上一个时刻有关（二者的加权平均）。即：$V_t = \beta V_{t-1} + (1 - \beta)\theta_t$，这里，$\theta_t$表示 t 时刻的测量值（即蓝色的点），$V_{t-1}$表示上一个时刻的计算值（即红色曲线的上一个值），$\theta$为加权参数。
Momentum 梯度下降
借助指数加权平均的思想，我们可以解决上面的抖动问题。即在SGD的基础上，加上了上一步的梯度：
$$v_t = \gamma v_{t-1} + (1 - \gamma)\nabla_{\theta}{J(\theta)}$$
$$\theta = \theta - \alpha v_t$$
其中$\gamma$通常设为0.9。由于目标函数在Y方向上摇摆，所以前后两次计算的梯度在Y方向上相反，所以相加后相互抵消，而X方向上梯度方向不变，所以X方向的梯度是累加的，其效果就是损失函数在Y方向上的震荡减小了，而更加迅速地从X方向接近最优点。如图所示：
也可以把这个过程和在山坡放一个球让其滚下类比：当从山顶释放一个小球时，由于重力的作用小球滚下的速度会越来越快；与此类似，冲量的作用会使相同方向的梯度不断累加，不同方向的梯度相互抵消，其效果就是逼近最优点的速度不断加快。
Nesterov Accelerated Gradient
但是上面，小球越来越快的往山谷滚动，越接近谷底越快，会导致冲过谷底。因此我们需要让小球感知坡度的变化，从而在它再次冲上山坡之前减速而避免错过山谷。NAG方法更新梯度的公式变为：
$$v_t = \gamma v_{t-1} + (1 - \gamma)\nabla_{\theta}{J(\theta - \gamma v_{t-1})}$$
$$\theta = \theta - \alpha v_t$$
即在 Momentum 的基础上，进行修正，达到减速的效果。
Adagrad
我们除了想让参数更新速率自适应坡度外，还需要适合处理稀疏特征的梯度更新算法。比如，稀疏特征采用高的更新速率，其他特征采用相对较低的更新速率。Adagrad是一种适合处理稀疏特征的梯度更新算法，它对稀疏特征采用高的更新速率，而对其他特征采用相对较低的更新速率。Dean等人发现Adagrad能很好地提高SGD的鲁棒性，它已经被谷歌用来训练大规模的神经网络。
Adagrad对每个参数使用不同的参数进行更新。如果用$g_{t,i}$来表示参数$\theta_i$在第t次更新时的梯度，即$g_{t,i} = \nabla_{\theta}{J(\theta_i)}$，则SGD的更新规则可以写作：
$$\theta_{t+1, i} = \theta_i - \alpha g_{t,i}$$
而Adagrad的更新规则可以表示为：
$$\theta_{t+1, i} = \theta_i - \frac{\alpha}{\sqrt{G_{t,ii} + \epsilon}} g_{t,i}$$
其中，$G_{t,ii}$是一个$\mathbb{R}^{d×d}$维的对角矩阵，其第i行第i列的元素为过去到当前第i个参数的梯度平方和，$\epsilon$是为了防止分母为0的平滑项。进一步，可以将上式向量化如下：
$$\theta_{t+1} = \theta_i - \frac{\alpha}{\sqrt{G_{t} + \epsilon}} \bigodot g_{t}$$
这样，利用Adagrad就可以自动根据每个特征的稀疏性来设置不同的学习率。但是$G_t$累加了参数的历史梯度的平方，所以到后期学习率会越来越小，最后无法再学习到新的信息。
Adadelta
Adadelta 和 Adagrad 的主要区别就是把 $G_t$变为$E[g^2]_t$，即不再累加参数所有的历史梯度平方和，转而设定一个窗口w，只求前w个历史梯度平方的平均数。而$E[g^2]t = \beta E[g^2]{t-1} + (1-\beta)g_t^2$，因此Adadelta更新规则可以写作：
$$\theta_{t+1} = \theta_i - \frac{\alpha}{\sqrt{E[g^2]t + \epsilon}} \bigodot g{t}$$
RMSprop
RMSprop（Root Mean Square prop）由Hinton提出，实际上是Adadelta的一种特殊形式：
$$E[g^2]t = \beta E[g^2]{t-1} + (1-\beta)g_t^2$$
$$\theta_{t+1} = \theta_t - \frac{\alpha}{\sqrt{E[g^2]t} + \epsilon} \bigodot g{t}$$
Adam
Adam的全称是Adaptive Moment Estimation, 它也是一种自适应学习率方法。可以把它看做 RMSprop 和 Momentum 的结合。
$$m_t = \beta_1 m_{t - 1} + (1 - \beta_1)g_t$$
$$v_t = \beta_2 v_{t - 1} + (1 - \beta_2)g_t^2$$
$m_t$,$v_t$分别是梯度的带权平均和带权有偏方差，由于当$\beta_1$,$\beta_2$接近于1时，这两项接近于0，因此对他们进行了偏差修正：
$$\hat{m_t} = \frac{m_t}{1 - \beta_1^t}$$
$$\hat{v_t} = \frac{v_t}{1 - \beta_2^t}$$
最终更新方程为：
$$\theta_{t+1} = \theta_t - \frac{\alpha}{\sqrt{\hat{v_t}} + \epsilon} \bigodot m_{t}$$
一般将$\beta_1$设为0.9,$\beta_2$设为0.999, $\epsilon$设为10−8。一般在深度学习的梯度优化中，会使用 Adam。
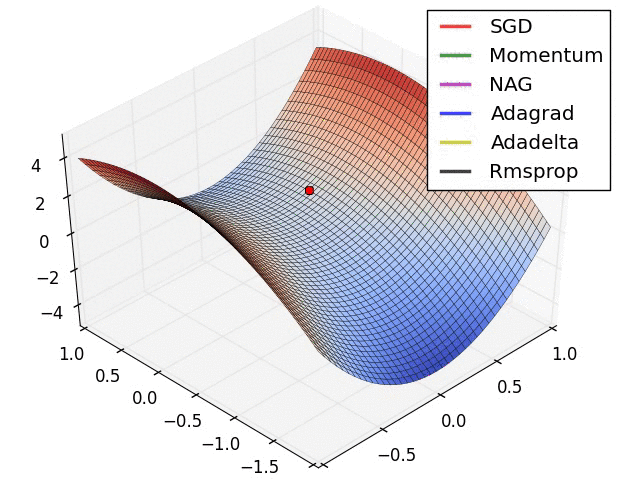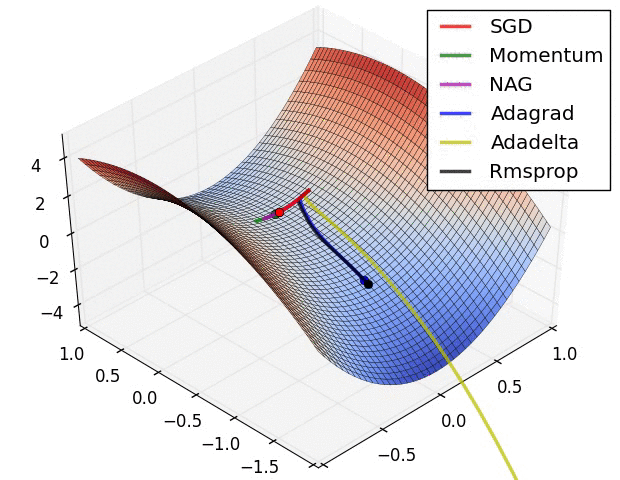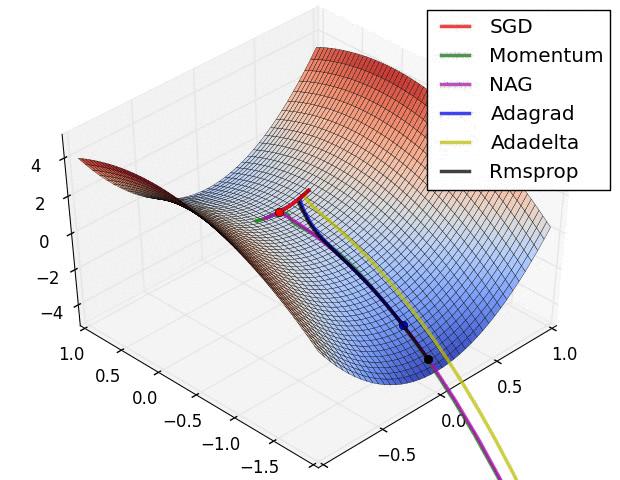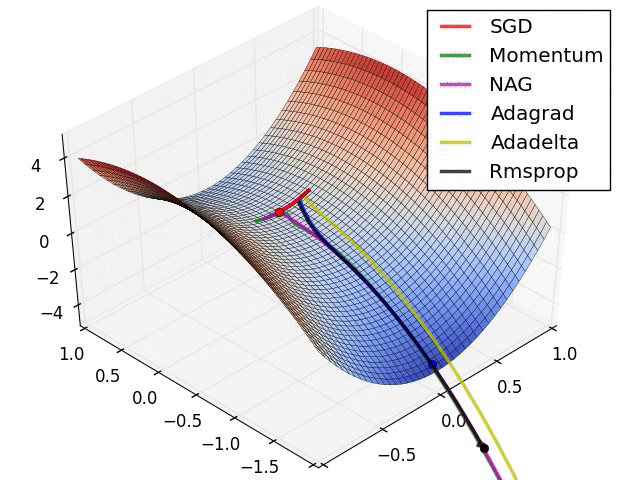
几种算法的效果对比
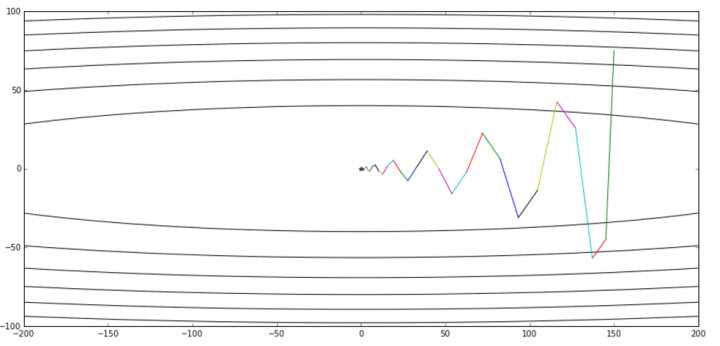
如图所示，所有方法都从相同位置出发，经历不同的路径到达了最小点，其中Adagrad、Adadelta和RMSprop一开始就朝向正确的方向并且迅速收敛，而冲量、NAG则会冲向错误的方向，但是由于NAG会向前多“看”一步所以能很快找到正确的方向。
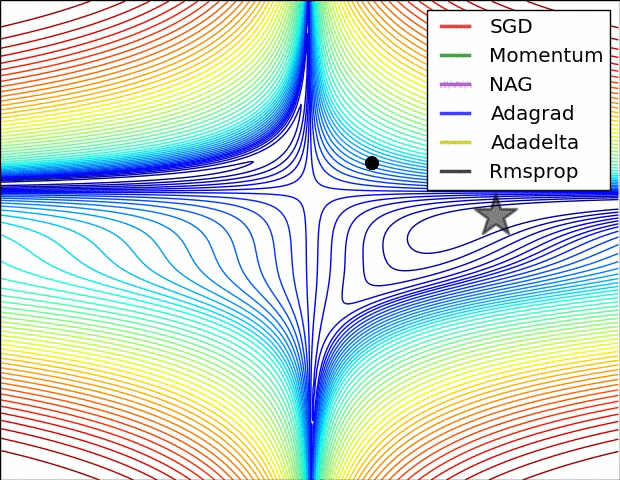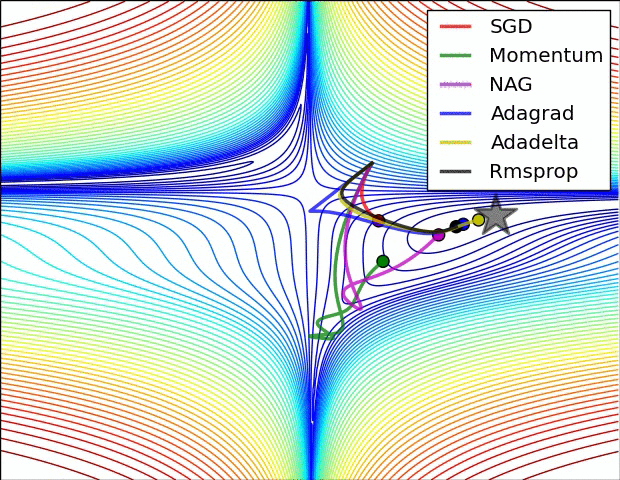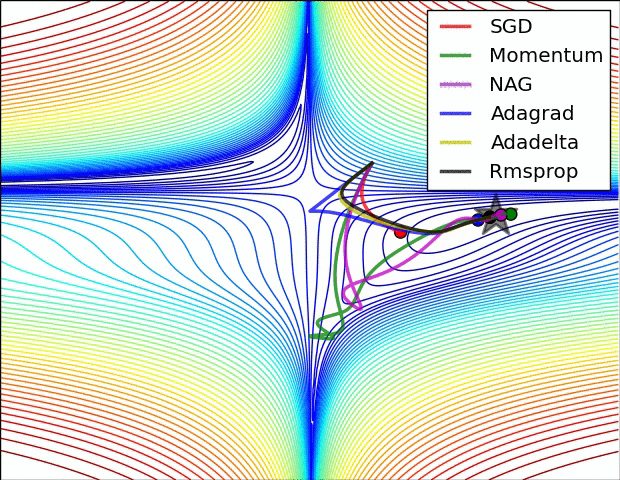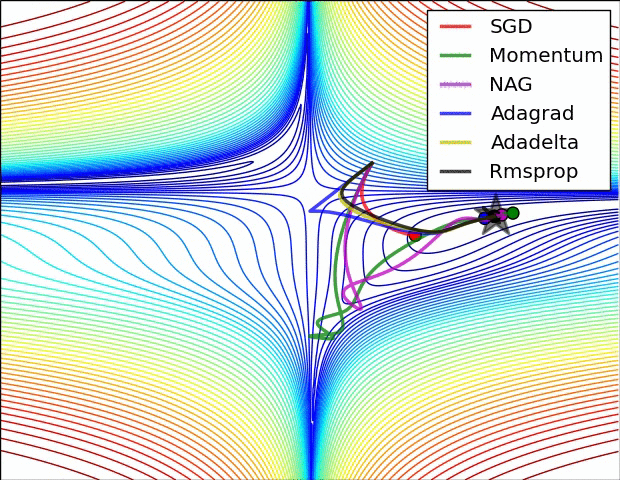下图显示了这些方法逃离鞍点的能力，鞍点有部分方向有正梯度另一些方向有负梯度，SGD方法逃离能力最差，冲量和NAG方法也不尽如人意，而Adagrad、RMSprop、Adadelta很快就能从鞍点逃离出来。
