统计学习方法(笔记)-逻辑斯谛回归与最大熵模型
逻辑斯谛回归(Logistic regression)是统计学习中的经典分类方法,最大熵是概率模型学习的一个准则,将其推广到分类问题得到最大熵模型。逻辑斯谛回归模型与最大熵模型都是属于对数线性模型。
逻辑斯谛回归模型
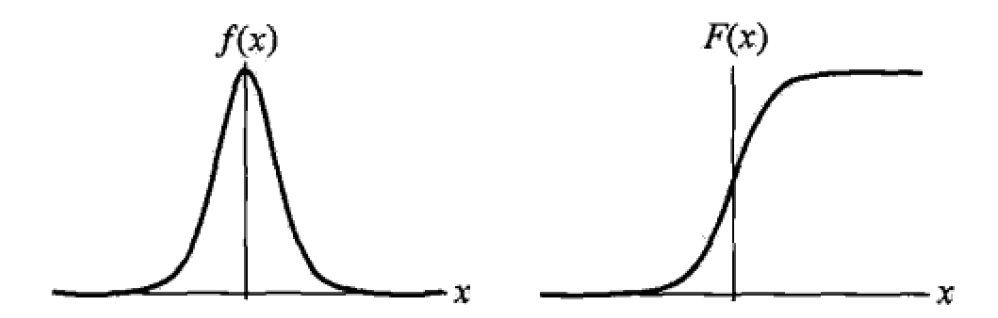
逻辑斯谛分布的分布函数和密度函数如下:
$$F(x) = P(X <= x) = \frac{1}{1+e^{-(x - \mu) / \gamma}}$$
$$f(x) = F’(x) = \frac{e^{-(x-\mu) / \gamma}}{\gamma (1+e^{-(x-\mu) / \gamma})^2}$$
其中$\mu$为位置参数;$\gamma > 0$为形状参数,值越小,分布越集中于$\mu$附近。其分布的密度函数与分布函数如图:
二项逻辑斯谛回归模型是如下的条件概率分布:
$$P(Y=1|x) = \frac{exp(w \cdot x + b)}{1+ exp(w \cdot x + b)}$$
$$P(Y=0|x) = \frac{1}{1+ exp(w \cdot x + b)}$$
逻辑斯谛回归模型是指,输出$Y=1$的对数几率,其是由输入$x$的线性函数表示的模型。可以用极大似然估计法估计模型参数,从而得到逻辑斯谛回归模型。学习过程通常采用的方法是梯度下降法及拟牛顿法。
最大熵模型
最大熵原理认为,学习概率模型时,在所有可能的概率模型(分布)中,熵最大的模型是最好的模型。通常用约束条件来确定概率模型的集合,所以最大熵原理也可以表述为在满足约束条件的模型集合汇总选取熵最大的模型。最大熵模型的学习可以形式化为约束最优化问题:
$$\max_{P \in C} H(P) = - \sum_{x,y}\tilde{P}(x)p(y|x)logP(y|x)$$
$$s.t. \qquad E_p(f_i) = E_\tilde{p}(f_i) $$
$$\qquad \sum_yP(y|x)=1$$
最大熵模型是由以下条件概率分布表示的分类模型:
$$P_w(y|x) = \frac{1}{Z_w(x)}exp(\sum_{i=1}^{n}w_if_i(x,y))$$
$$Z_w(x)=\sum_yexp(\sum_{i=1}^{n}w_if_i(x,y))$$
其中$Z_w(x)$是规范化因子,$f_i$为特征函数,$w_i$为特征的权值。
逻辑斯谛回归模型与最大熵模型都属于对数线性模型。二者的学习一般采用极大似然估计,或正则化的极大似然估计。逻辑斯谛回归模型及最大熵模型学习可以形式化为无约束最优化问题。求解该最优化问题的算法有改进的迭代尺度法、梯度下降法、拟牛顿法。