By

 

文章目录
  1. 1. 初始化为0
  2. 2. 随机初始化
  3. 3. Xavier initialization
  4. 4. He initialization
  5. 5. Batch Normalization Layer

调参对深度学习的效果异常重要，甚至经常开玩笑说这是一门调参工程学。而 Weight Initialization 对模型收敛速度和模型质量有重要影响。

Deep-Learning # 深度学习的参数

深度学习的参数分为超参（hyper parameters）和普通参数。超参是模型开始训练前，人工指定的参数，比如网络的层数、每层的神经元数、学习速率以及正则项系数等。超参对模型的效果非常重要。而普通参数，就是通常的 W 以及 b。深度学习模型的本质过程就是对权重（W）进行更新。而在开始训练神经网络前，需要初始化 W 以及 b 的值，这个初始值会影响模型训练的收敛速度以及质量。本文主要讲解 W 的初始化。

初始化为0

如图所示一个简单的神经网络，有一个中间层，中间层有两个神经元。

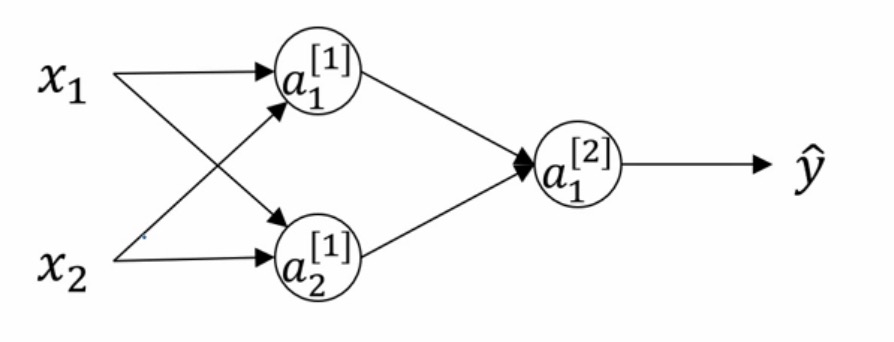如果我们初始化权重： $W^{[1]}=\begin{bmatrix} 0&0\\\ 0&0 \end{bmatrix}$或者任意上下神经元权重相同，由于对称性，通过激活函数得到的值相同，并且通过梯度下降，更新后的权重也相同。因此无论进行多少次迭代，二者的权重依然保持不变，这种情况下，多个隐藏单元就会没有意义。 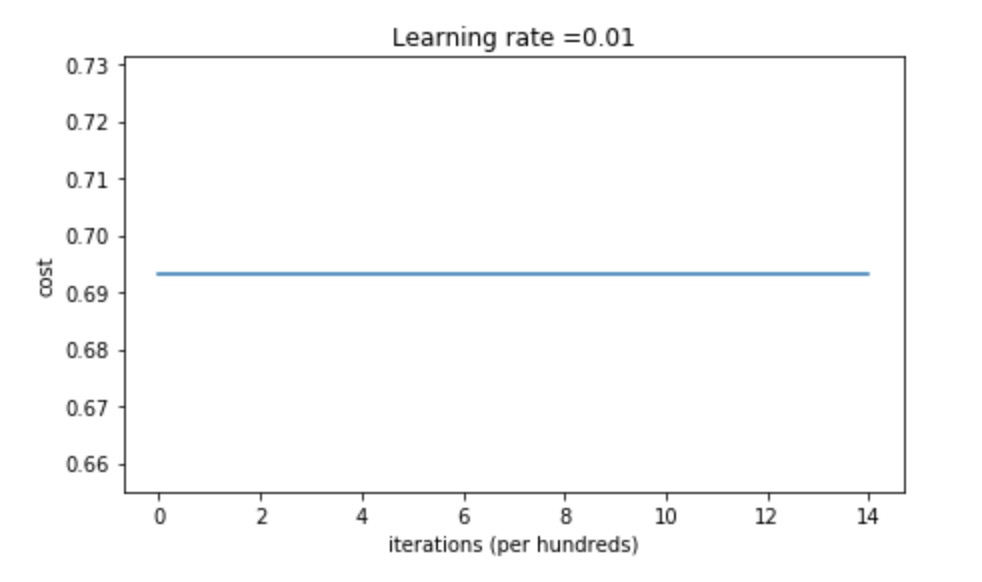初始化为0的损失 上图为一个初始化权重为0的神经网络的损失函数值变化，可以看出，损失值并没有变化。 通常来说，将权重都设置为0，意味着每层网络中的神经元都一样，等同于每层只有一个神经元，其效果并不会比线性分类器（如逻辑回归）好。

随机初始化

如果我们将权重初始化为随机数，比如：np.random.randn(layers_dims[l], layers_dims[l - 1]) * 0.01

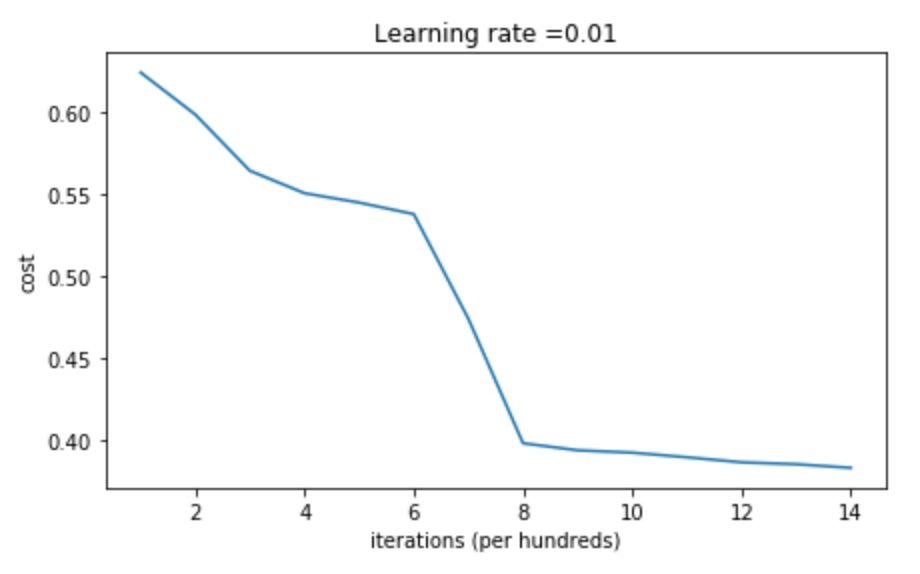随机初始化的损失 可以看到，随着训练，损失值逐渐变小，但是最终的损失值依然比较高。但是随着层数的增加，会导致梯度消失。如果增大随机初始化的值，比如将0.01变为10，会发现依然会出现梯度消失，参数难以被继续更新。

Xavier initialization

上述问题可以使用Xavier initialization 解决。Xavier 初始化的基本思想是保持输入和输出的方差一致。即将随机初始化的值乘以缩放因子：$\sqrt{\frac{1}{layers_dims[l-1]}}$。也就是将参数初始化变为：np.random.randn(layers_dims[l], layers_dims[l - 1]) * np.sqrt(1. / layers_dims[l - 1])

Xavier初始化是在线性函数上推导得出的，它能够保持输出在很多层之后依然有着良好的分布，如图为使用 tanh 激活函数后的输出概率分布：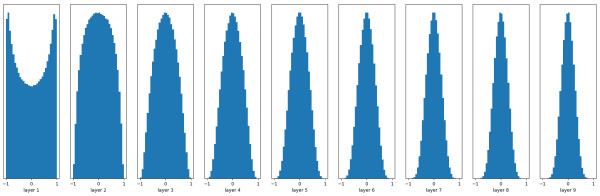
Xavier初始化在tanh的输出概率分布
但是其对于 ReLU 的效果并不好，如图：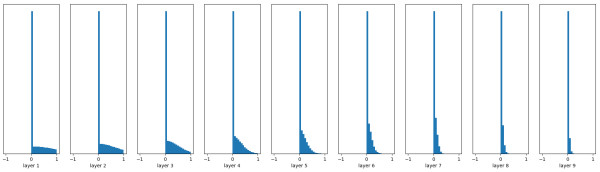
Xavier初始化在ReLU的输出概率分布

He initialization

He 初始化可以解决上面在 ReLU 激活函数时 Xavier 效果不好的问题。其思想是：在ReLU网络中，假定每一层有一半的神经元被激活，另一半为0，所以，要保持方差不变，只需要在 Xavier 的基础上再除以2。即缩放因子变为：$\sqrt{\frac{2}{layers_dims[l-1]}}$，初始化代码为：np.random.randn(layers_dims[l], layers_dims[l - 1]) * np.sqrt(2. / layers_dims[l - 1])

其分布如下图，可见效果很好。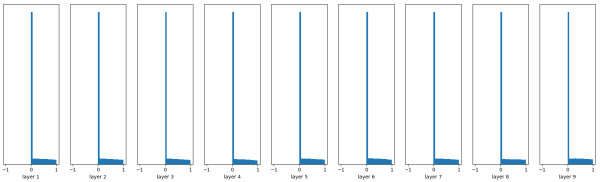
He初始化在ReLU的输出概率分布
其损失如图所示：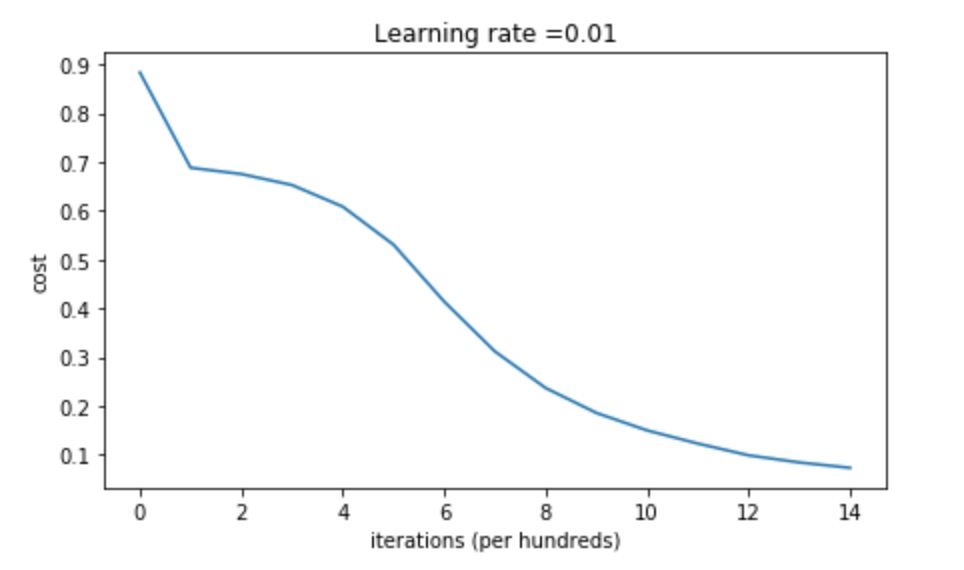
He初始化的损失

Batch Normalization Layer

If you want it, just make it! 合理的参数初始化是为了避免梯度消失，有效的反向传播，需要进入激活函数的数值有一个合理的分布，以便于反向传播时计算梯度。其思想就是在线性变化和非线性激活函数之间，将数值做一次高斯归一化和线性变化。
He初始化的损失
Batch Normalization中所有的操作都是平滑可导，因此可以有效的学习到参数$\gamma$，$\beta$。需要注意的是，训练时的$\gamma$，$\beta$由当前batch计算得出，而测试时$\gamma$，$\beta$使用训练时保存的均值。

如图表示使用随机初始化的参数，ReLU 作为激活函数，未使用 Batch Normalization 时，每层激活函数的输出分布：

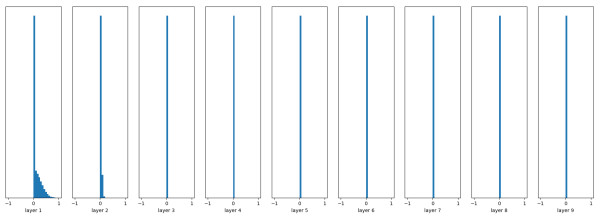未使用BatchNormalization 下图为使用 Batch Normalization 时，每层激活函数的输出分布： 使用BatchNormalization 可见，使用 Batch Normalization 非常有效。

#参考资料

  1. Glorot X, Bengio Y. Understanding the difficulty of training deep feedforward neural networks[C]//Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics. 2010: 249-256.
  2. He K, Zhang X, Ren S, et al. Delving deep into rectifiers: Surpassing human-level performance on imagenet classification[C]//Proceedings of the IEEE international conference on computer vision. 2015: 1026-1034.
  3. Ioffe S, Szegedy C. Batch normalization: accelerating deep network training by reducing internal covariate shift (2015)[J]. arXiv preprint arXiv:1502.03167, 1735-1780.
  4. Coursera, deep-neural-network
文章目录
  1. 1. 初始化为0
  2. 2. 随机初始化
  3. 3. Xavier initialization
  4. 4. He initialization
  5. 5. Batch Normalization Layer